A)
B) 1
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the exact value of the expression. -
A) 1
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If n is an integer, n ∙ 180° represents an integer multiple of 180°, and (2n + 1) ∙ 90° represents an odd integer multiple of 90°. Decide whether the expression is equal to 0, 1, -1, or is undefined. -
A) 0
B)
C) Undefined
D) 1
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Decide whether the statement is possible or impossible for an angle θ. -
A) Possible
B) Impossible
D) undefined
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the expression. -
A)
B)
C) Undefined
D) 0
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the fundamental identities to find the value of the trigonometric function. -Find , given that and is in quadrant IV.
A)
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the fundamental identities to find the value of the trigonometric function. -Find , given that and is in quadrant .
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-A -ft fence is away from a plant in the direction of the sun. It is observed that the shadow of the fence extends exactly to the bottom of the plant. (See drawing) Find , the angle of elevation of the sun at that time. Round the measure of the angle to the nearest tenth of a degree when necessary.
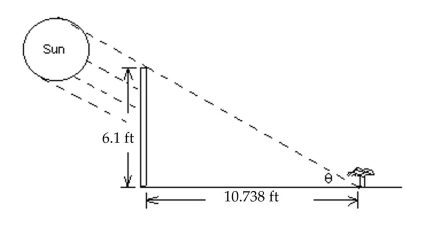
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the reference angle for the given angle. -
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If r is a positive number and the point (x, y) is in the indicated quadrant, decide whether the given ratio is positive or negative. -II,
A) Negative
B) Positive
D) undefined
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the fundamental identities to find the value of the trigonometric function. -Find , given that and is in quadrant II.
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the signs of the given trigonometric functions of an angle in standard position with the given measure. - and
A) negative and negative
B) positive and negative
C) negative and positive
D) positive and positive
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem for the given information. -Find the equation of a line passing through the origin so that the cosine of the angle between the line in quadrant and the positive -axis is .
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize the denominator if applicable. -Find when and
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Decide whether the statement is possible or impossible for an angle θ. - and
A) Impossible
B) Possible
D) undefined
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch an angle in standard position such that has the least positive measure and the given point is on the terminal
side of
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find all values of θ, if θ is in the interval [0, 360°) and has the given function value. - is undefined
A)
B) and
C)
D) and
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the appropriate identity to find the indicated function value. Rationalize the denominator, if applicable. If the given value is a decimal, round your answer to three decimal places. - , given that
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -Radio direction finders are set up at points and apart on an east-west line. From it is found that the bearing of a signal from a transmitter is , while from it is . Find the distance of the transmitter from B, to the nearest hundredth of a mile.
A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the fundamental identities to find the value of the trigonometric function. -Find , given that and is in quadrant IV.
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Showing 81 - 100 of 301
Related Exams